Electron Transitions

Hydrogen Energy Levels

This Bohr model picture of the orbits has some usefulness for visualization so long as it is realized that the "orbits" and the "orbit radius" just represent the most probable values of a considerable range of values. If the radial probabilities for the states are used to make sure you understand the distributions of the probability, then the Bohr picture can be superimposed on that as a kind of conceptual skeleton.

Hydrogen Energy Level Plot

The basic structure of the hydrogen energy levels can be calculated from the Schrodinger equation. The energy levels agree with the earlier Bohr model, and agree with experiment within a small fraction of an electron volt.

If you look at the hydrogen energy levels at extremely high resolution, you do find evidence of some other small effects on the energy. The 2p level is split into a pair of lines by the spin-orbit effect. The 2s and 2p states are found to differ a small amount in what is called the Lamb shift. And even the 1s ground state is split by the interaction of electron spin and nuclear spin in what is called hyperfine structure.

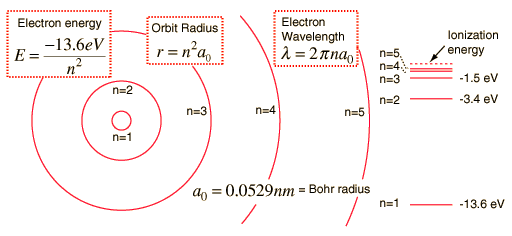
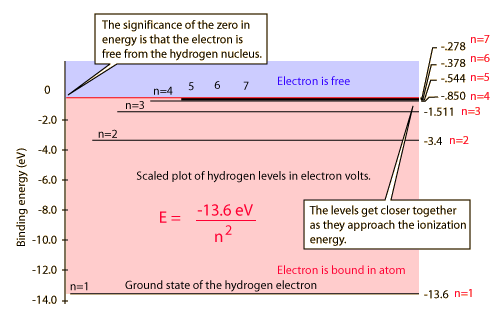
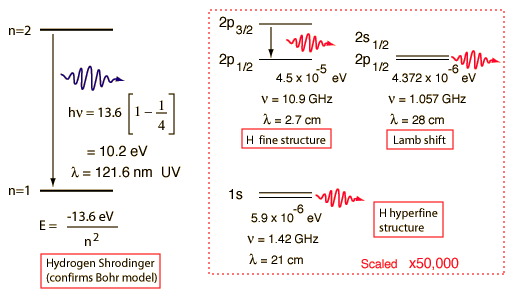
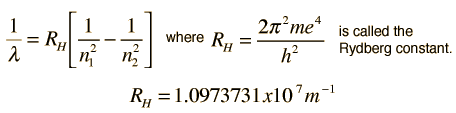Hydrogen Spectrum

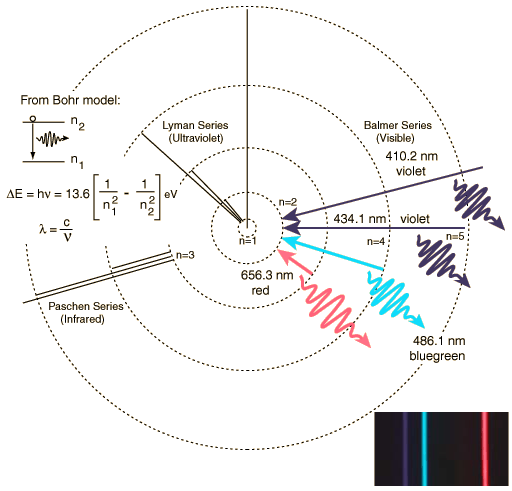
This spectrum was produced by exciting a glass tube of hydrogen gas with about 5000 volts from a transformer. It was viewed through a diffraction grating with 600 lines/mm. The colors cannot be expected to be accurate because of differences in display devices.

At left is a hydrogen spectral tube excited by a 5000 volt transformer. The three prominent hydrogen lines are shown at the right of the image through a 600 lines/mm diffraction grating. An approximate classification of spectral colors: Violet (380-435nm) Blue(435-500 nm) Cyan (500-520 nm) Green (520-565 nm) Yellow (565- 590 nm) Orange (590-625 nm) Red (625-740 nm)

Radiation of all the types in the electromagnetic spectrum can come from the atoms of different elements. A rough classification of some of the types of radiation by wavelength is:

• Infrared   > 750 nm
• Visible   400 - 750 nm
• Ultraviolet   10-400 nm
• Xrays   < 10 nm

Measured Hydrogen Spectrum

Wavelength (nm) Relative Intensity Transition Color 383.5384 5 9 -> 2 Violet 388.9049 6 8 -> 2 Violet 397.0072 8 7 -> 2 Violet 410.174 15 6 -> 2 Violet 434.047 30 5 -> 2 Violet 486.133 80 4 -> 2 Bluegreen (cyan) 656.272 120 3 -> 2 Red 656.2852 180 3 -> 2 Red