Even and Odd Functions

A function y= g(x) is even if g(-x) = g(x). Its graph is symmetric with respect to the y axis. A function y=h(x) is odd if h(-x) = -h(x) . Its graph is antisymmetric with respect to the y axis.

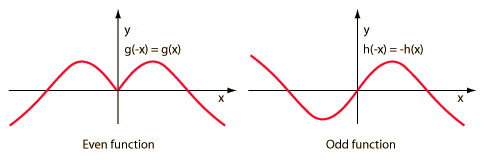
Kreyszig list three key facts about even and odd functions.
1. If g(x) is an even function, then

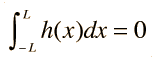
Some important applications involve the trigonometric functions. The function cos nx is even and sin nx is odd. The calculation of AC electric power makes use of these properties to arrive at an expression for average power.