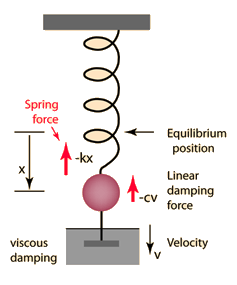
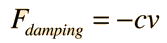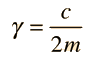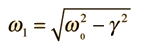Damped Harmonic Oscillator

Damping coefficient Undamped oscillator Driven oscillator

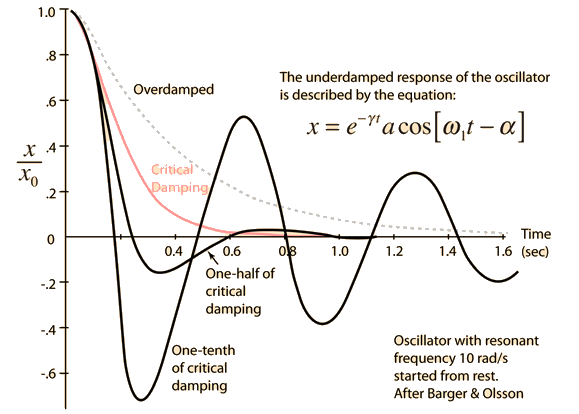
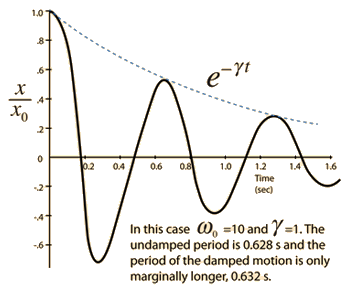
The Newton's 2nd Law motion equation is 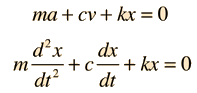This is in the form of a homogeneous second order differential equation and has a solution of the form 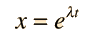Substituting this form gives an auxiliary equation for λ 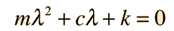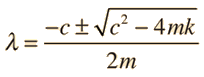The roots of the quadratic auxiliary equation are The three resulting cases for the damped oscillator are

Damping Coefficient

When a damped oscillator is subject to a damping force which is linearly dependent upon the velocity, such as viscous damping, the oscillation will have exponential decay terms which depend upon a damping coefficient. If the damping force is of the form

then the damping coefficient is given by

This will seem logical when you note that the damping force is proportional to c, but its influence inversely proportional to the mass of the oscillator.

Underdamped Oscillator

For any value of the damping coefficient γ less than the critical damping factor the mass will overshoot the zero point and oscillate about x=0. The behavior is shown for one-half and one-tenth of the critical damping factor. Also shown is an example of the overdamped case with twice the critical damping factor.

Underdamped Oscillator

The equation is that of an exponentially decaying sinusoid. The damping coefficient is less than the undamped resonant frequency . The sinusoid frequency is given by but the motion is not strictly periodic.