Barrier Penetration

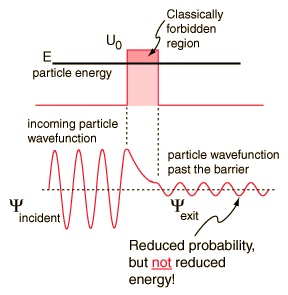According to classical physics, a particle of energy E less than the height U0 of a barrier could not penetrate - the region inside the barrier is classically forbidden. But the wavefunction associated with a free particle must be continuous at the barrier and will show an exponential decay inside the barrier. The wavefunction must also be continuous on the far side of the barrier, so there is a finite probability that the particle will tunnel through the barrier.

As a particle approaches the barrier, it is described by a free particle wavefunction. When it reaches the barrier, it must satisfy the Schrodinger equation in the form

which has the solution

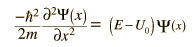
Note that in addition to the mass and energy of the particle, there is a dependence on the fundamental physical constant Planck's constant h. Planck's constant appears in the Planck hypothesis where it scales the quantum energy of photons, and it appears in atomic energy levels which are calculated using the Schrodinger equation.

If a particle of energy E =x10^ joules = eV =MeV =GeV

and mass

m = x 10^ kg = me = mp = MeV/c2,

approaches a barrier of height

U0 = x 10^ joule = eV= MeV,

and thickness

d = x 10^ m = nm= fermi,

then the attenuation factor is

a = x10^ 1/m .

and the ratio of the exit and incident amplitudes is x10^ .

Since the probability is proportional to the square of the amplitude, the tunneling probability is x10^ .

Alpha decay barrier
 Index

Schrodinger equation concepts
 
HyperPhysics***** Quantum Physics R Nave
 Go Back