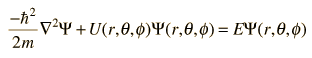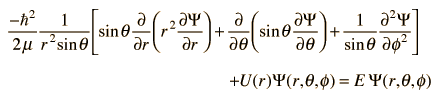3-D Schrodinger Equation

In three dimensions, the time-independent Schrodinger equation takes the form


for cartesian coordinates. This can be written in a more compact form by making use of the Laplacian operator


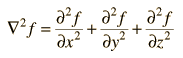
The Schrodinger equation can then be written:


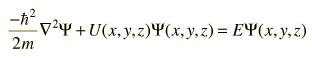
For systems with a spherically symmetric potential, like the hydrogen atom, it is advantageous to use spherical coordinates.

Index

Schrodinger equation concepts
  HyperPhysics***** Quantum Physics Go Back





Schrodinger Equation, Spherical Coordinates

If the potential of the physical system to be examined is spherically symmetric, then the Schrodinger equation in spherical polar coordinates can be used to advantage. For a three-dimensional problem, the Laplacian in spherical polar coordinates is used to express the Schrodinger equation in the condensed form

Expanded, it takes the form

This is the form best suited for the study of the hydrogen atom. 		Index

Schrodinger equation concepts
  HyperPhysics***** Quantum Physics Go Back