Uncertainty Principle Application: Particle in a 3-D Box

An important idea which arises from quantum theory is that it requires a large amount of energy to contain a particle in a small volume. This idea arises in the treatment of the "particle in a box" with the Schrodinger equation, and the same idea is found by applying the uncertainty principle.

Consider a particle of mass m which is confined to a three dimensional box of side length L but free to move within the box. The uncertainty principle can be used to estimate the minimum value of average kinetic energy for such a particle.

Taking the uncertainty in position in one dimension as its root-mean-square deviation:

Show

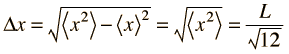then the uncertainty in momentum is

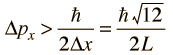
The average kinetic energy can be expressed in terms of the average of the momentum squared, which is related to the uncertainty in momentum by

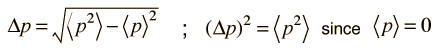
The average momentum is zero for free random motion of the particle in a box. The y and z coordinates are equivalent, so the average kinetic energy can be expressed as

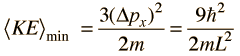
For this three-dimensional particle in a box , for a box of dimension