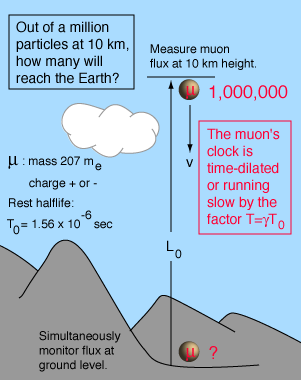
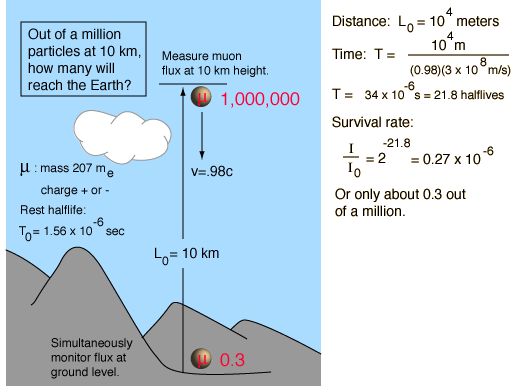
Muon Experiment
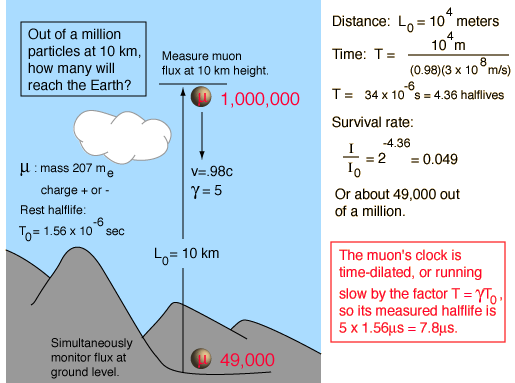
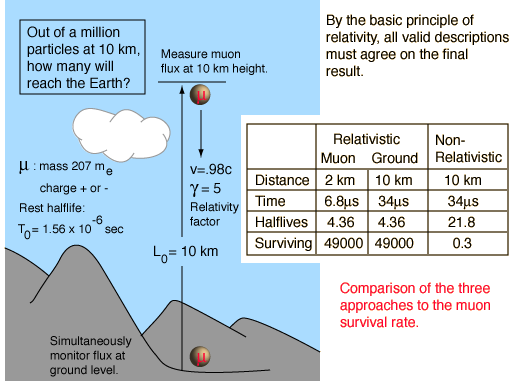
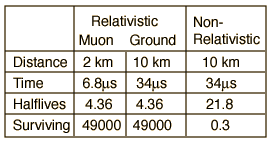
The measurement of the flux of muons at the Earth's surface produced an early dilemma because many more are detected than would be expected, based on their short half-life of 1.56 microseconds. This is a good example of the application of relativistic time dilation to explain the increased particle range for high-speed particles.
Non-Relativistic
 | Non-relativistic |  | Relativistic, Earth observer |  | Relativistic, muon observer |
 | Comparison |  | Comments on comparison |  | Vary parameters |
| A brief overview of time. |
Relativity concepts
| HyperPhysics***** Relativity | R Nave |