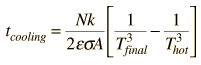Radiative Cooling of a Volcanic Fragment

The radiative cooling time for the ideal case of an object which remains at a uniform temperature with no limitation from heat transfer from the interior of the object is given by :

It must be kept in mind that for macroscopic objects, the calculated cooling time for the object as a whole will always be shorter than the real cooling time, so that it gives a lower bound. The above relationship assumes infinite thermal conductivity so that the temperature of the whole object is equal to the surface temperature. In the real world, the surface will cool faster than the interior. The rate of heat transfer from the interior will be expected to limit the rate of radiative loss from the surface.

Despite all these real-world limitations, it is interesting to try to model the process of the cooling of a hot object. Dr. Pam Burnley of GSU's Geology Department has a fragment of basaltic material which she found some 60 meters from the top of a small volcanic cone. The material has the appearance of having been ejected in an almost liquid state, but upon impact,it just bent one end of the fragment. This seems to imply that during its flight out of the cone, it cooled enough to be partially solid before impact.

These two views of the fragment show the two sides and the general impression of something fairly soft which was bent upon impact. It looks like a kind of splash of the volcanic material. Dr. Burnley refers to it as a "bomb" from the volcano.

Basic data was collected for the sample. Its mass is 367.6 grams. It measured about 17cm long, 5.5cm across and about 3.5cm thick. Submerged in water, its effective mass was 161 grams, so by Archimedes principle, its volume is 206.6 cm³. This gives a density of 1.78 gm/cm³, compared to a density of about 3 gm/cm³ for solid basalt, so there is a lot of air in it. Dr. Burnley estimated temperatures of about 1200 °C for the liquidus for this material and about 1000 °C for its solidus. So those seem to be plausible temperatures to use as the hot and cold temperatures for this modeling process.

Modeling the Radiative Cooling of a Hot Sphere

The modeling of the radiative cooling time of a hot sphere can give some insights into the role of radiation in cooling hot objects. Radiation is definitely not the only mechanism involved; the cooling of real macroscopic objects is a multifaceted topic including heat transfer from the interior of the object to the surface. With this caution about the applicability of these results to the real world, a model for the radiative cooling of a sphere will be developed. The model of the cooling time is given by

For a sphere of radius r = cm = m = x 10^m,

the surface area is A = cm^2 = x 10^ m^2.

the volume is V = cm^3 = x 10^ m^3.

If the density is gm/cm^3 = kg/m^3, then

the mass will be gm = kg = x10^ kg.

If the molar mass is known to be M = gm, then we can determine the number of atoms or molecules contained in the sphere. (Caution! These are assumed to be experimental numbers. Molar mass and density are not independent, and it is easy to choose values which are incompatible. Neither is the density precisely determined by the molar mass because of different crystal structures, etc. ). With these assumptions, the number of particles is modeled to be

= x10^

If the original high temperature is = K

then a cooling time of sec = x10^ sec

for an object with emissivity

corresponds to a final temperature K

In this calculation, the value of any parameter may be changed, and the default calculation will be the final temperature. However, if the final temperature is changed, the corresponding cooling time will be calculated.

While perhaps instructive as an exploration, this calculation is unrealistic because of several simplifying assumptions:

• The entire mass is presumed to be at the same temperature, whereas in any real object the surface will cool faster and you will have a lag in the transfer of heat from the interior of the object to the surface to be radiated.
• The effect of the ambient temperature is neglected. This may be justified. If the hot temperature is more than about three times the ambient, then the error from this assumption is down to 1%
• Other heat transfer process are neglected, namely conduction and convection. For temperatures over 1000K, this is probably justified. Conduction and convection depend linearly upon temperature, while radiation goes up according to the fourth power.
• The derivative of energy with respect to temperature above is highly simplified. This derivative is really the specific heat of the object, and it is more involved than this simple expression.