Coulomb Barrier for Fusion

In order to accomplish nuclear fusion, the particles involved must first overcome the electric repulsion to get close enough for the attractive nuclear strong force to take over to fuse the particles. This requires extremely high temperatures, if temperature alone is considered in the process. In the case of the proton cycle in stars, this barrier is penetrated by tunneling, allowing the process to proceed at lower temperatures than that which would be required at pressures attainable in the laboratory.

Considering the barrier to be the electric potential energy of two point charges (e.g., protons), the energy required to reach a separation r is given by

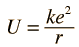	where k = Coulomb's constant and e is the proton charge.

Given the radius r at which the nuclear attractive force becomes dominant, the temperature necessary to raise the average thermal energy to that point can be calculated.

Calculation of Coulomb Barrier

The height of the Coulomb barrier can be calculated if the nuclear separation and the charges of the particle are known.

The temperature required to provide this energy as an average thermal energy for each particle would be

Critical Ignition Temperature for Fusion

The fusion temperature obtained by setting the average thermal energy equal to the coulomb barrier gives too high a temperature because fusion can be initiated by those particles which are out on the high-energy tail of the Maxwellian distribution of particle energies. The critical ignition temperature is lowered further by the fact that some particles which have energies below the coulomb barrier can tunnel through the barrier.

The presumed height of the coulomb barrier is based upon the distance at which the nuclear strong force could overcome the coulomb repulsion. The required temperature may be overestimated if the classical radii of the nuclei are used for this distance, since the range of the strong interaction is significantly greater than a classical proton radius. With all these considerations, the critical temperatures for the two most important cases are about:

The TFTR reached a temperature of 5.1 x 10⁸ K, well above the critical ignition temperature for D-T fusion.

Temperatures for Fusion

The temperatures required to overcome the coulomb barrier for fusion to occur are so high as to require extraordinary means for their achievement. Such thermally initiated reactions are commonly called thermonuclear fusion. Approximate temperatures are

In the sun, the proton-proton cycle of fusion is presumed to proceed at a much lower temperature because of the extremely high density and high population of particles.