Band Theory of Solids
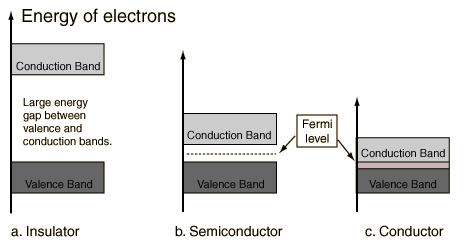
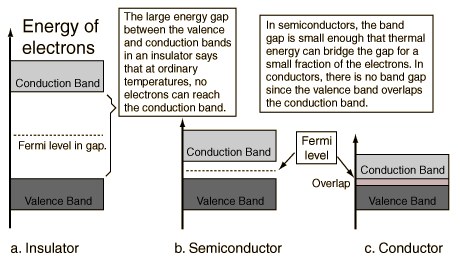
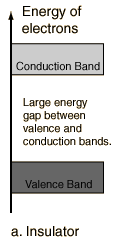
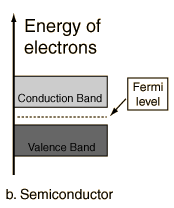
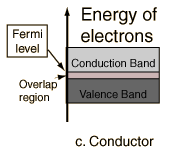
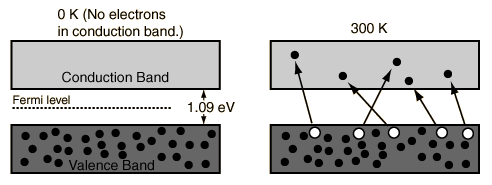
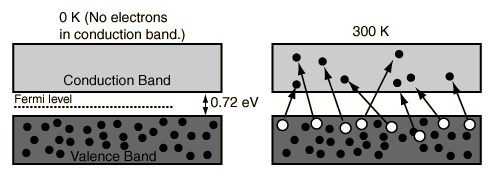
A useful way to visualize the difference between conductors, insulators and semiconductors is to plot the available energies for electrons in the materials. Instead of having discrete energies as in the case of free atoms, the available energy states form bands. Crucial to the conduction process is whether or not there are electrons in the conduction band. In insulators the electrons in the valence band are separated by a large gap from the conduction band, in conductors like metals the valence band overlaps the conduction band, and in semiconductors there is a small enough gap between the valence and conduction bands that thermal or other excitations can bridge the gap. With such a small gap, the presence of a small percentage of a doping material can increase conductivity dramatically.
An important parameter in the band theory is the Fermi level, the top of the available electron energy levels at low temperatures. The position of the Fermi level with the relation to the conduction band is a crucial factor in determining electrical properties.

| Closer look at bands | Band gap dependence on interatomic spacing |
Semiconductor concepts
Semiconductors for electronics
| HyperPhysics***** Condensed Matter | R Nave |